Linear Algebra - Khi cuộc đời cho bạn một quả trứng ?
Application of Linear Algebra in real life
Summary
Sau khi học xong môn đại số tuyến tính ở trường, tôi tự hỏi nó có tác dụng gì và vâng ngày hôm nay tôi đã tìm ra tác dụng của nó là … Xoay một quả trứng ???
Hả ? Quả trứng thì liên quan gì đến đại số tuyến tính ???. Chả là có một hôm, mình vô tình xem được video này trên youtube:
Why you NEED math for programming
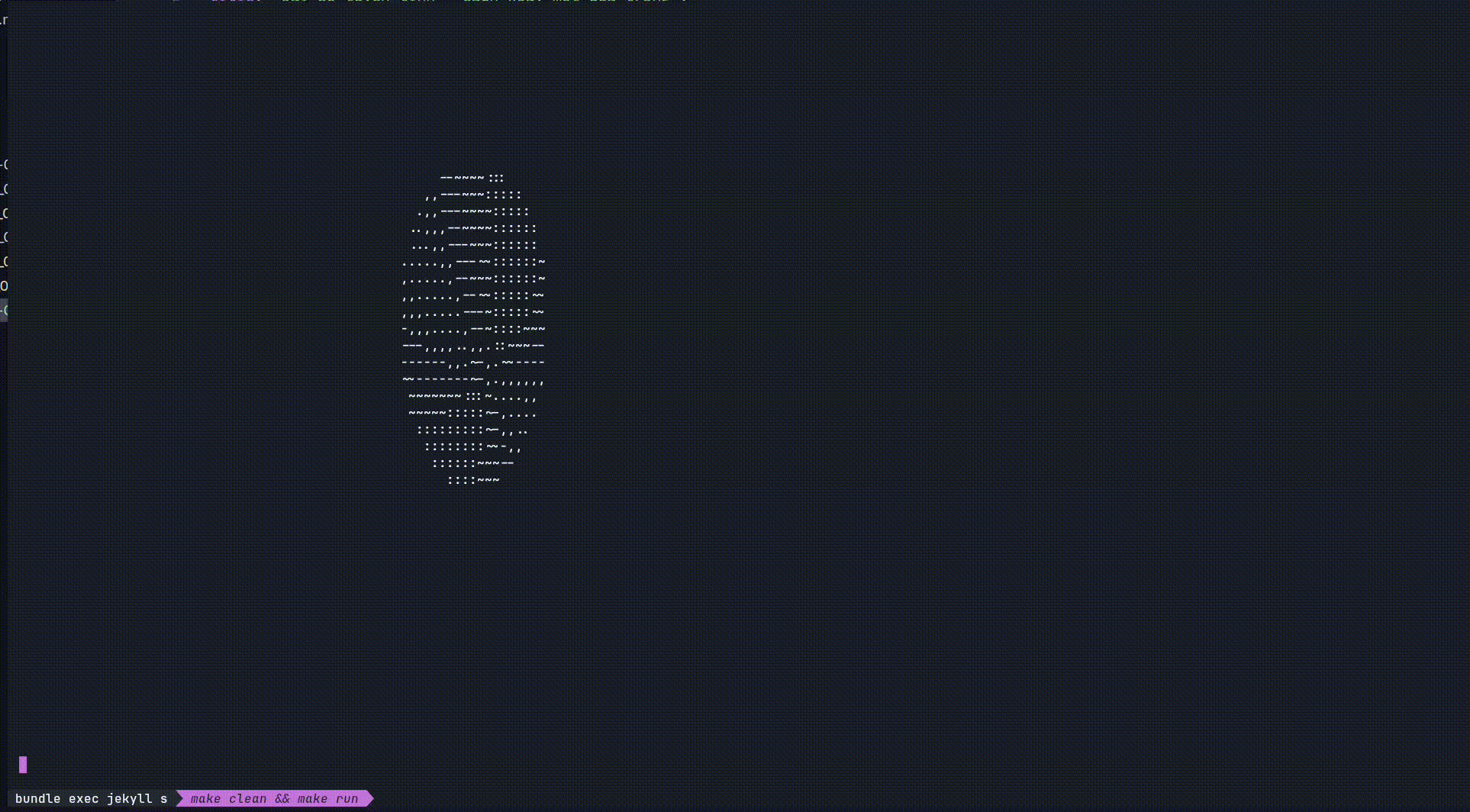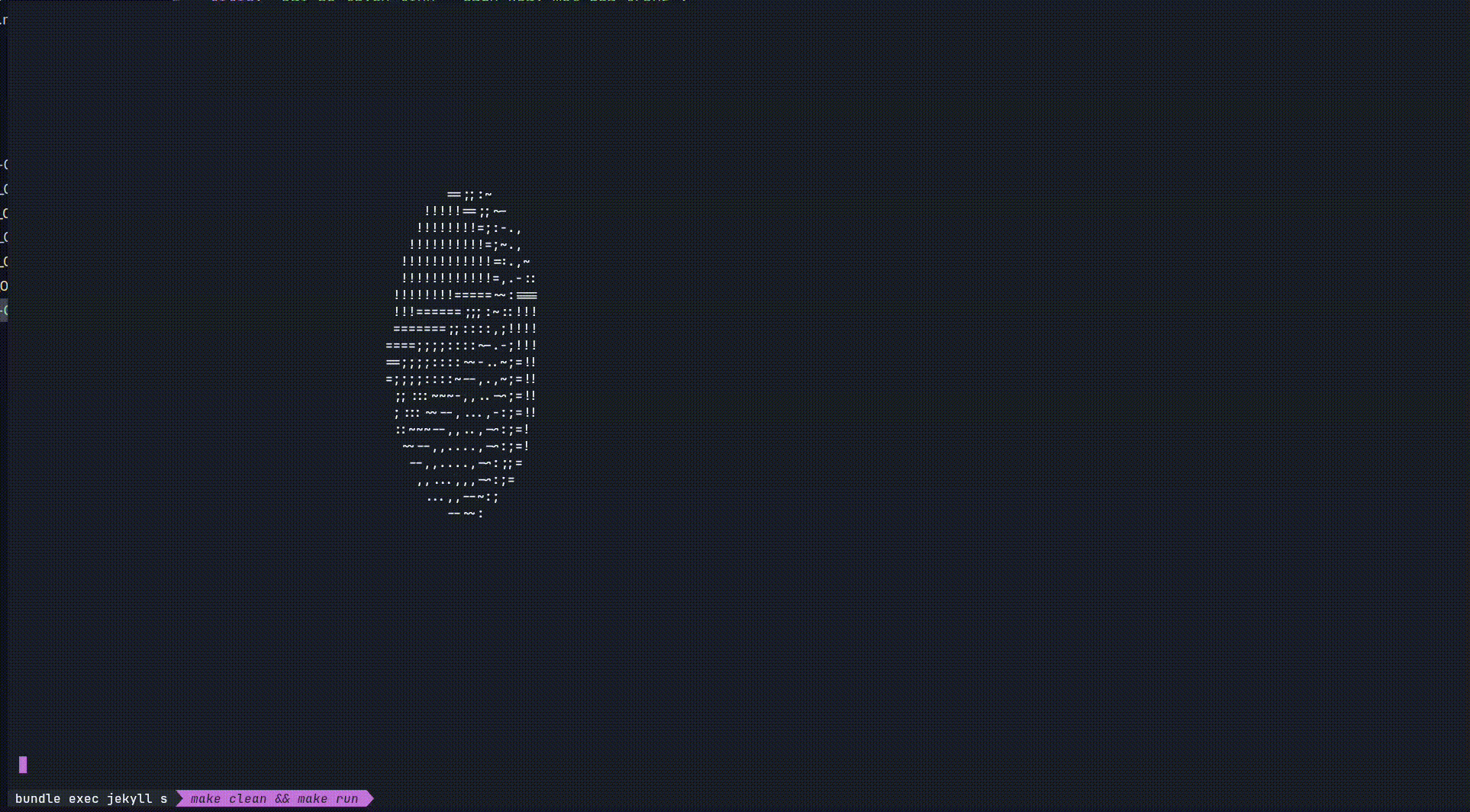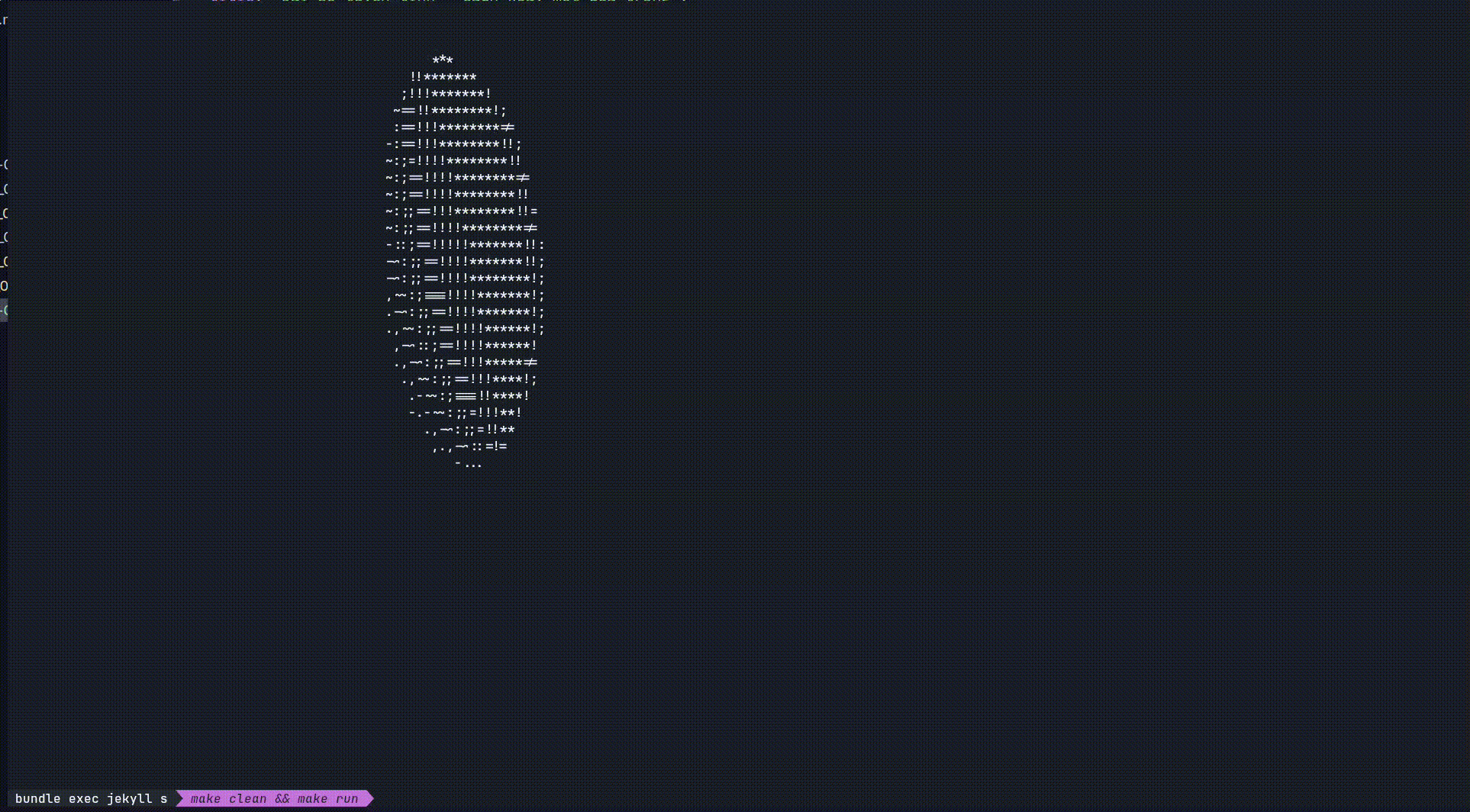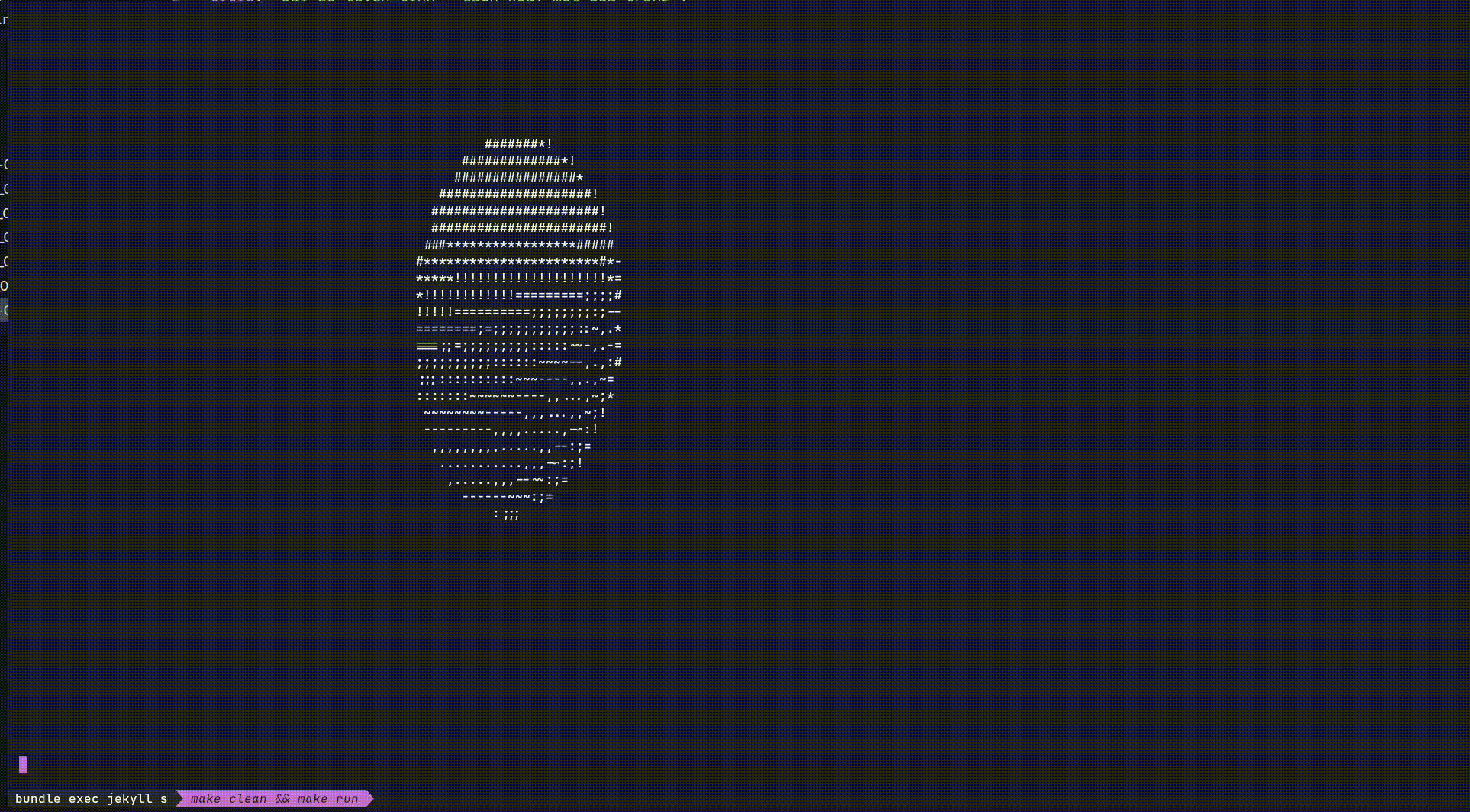
Tóm tắt đại khái thì: youtuber này (Joma Tech) đã nói về tầm quan trọng của toán trong lập trình. Cũng như anh ta đã làm được một chiếc doughnut 3D có thể xoay trên mặt phẳng 2D. Mình thấy hay hay nên quyết định tự làm cho mình một “quả trứng biết quay” và thành quả như này :D.
Mặc dù trông nó không giống 1 quả trứng cho lắm nhưng trong bài viết này, hãy cùng tìm hiểu cách để làm ra nó.
Từ mặt phẳng 2D đến không gian 3D
Đầu tiên, ta sẽ không sử dụng bất kì thư viện 3D nào hỗ trợ. Thứ duy nhất ta cần là ngôn ngữ C và một đống giấy nháp =)))).
Như các bạn đã biết, đối với một hình 3D đối xứng như hình cầu, hình bánh doughnut, hình trứng, … thì ta có thể biểu diễn trên không gian 3 chiều của nó chỉ với một phương trình mặt cắt. Thật vậy, ví dụ như với hình cầu, mặt cắt của nó là một đường tròn. Còn với hình trứng, mặt cắt của nó là một elip.
Có được mặt cắt này, việc của ta chỉ là cho mặt cắt này quay quanh một trục nào đó là xong. Các bạn có thể đọc thêm trang wiki về Solid of revolution Solid of revolution để hiểu rõ hơn về vấn đề này.
Như vậy đã xong, việc của ta bây giờ là đi tìm một phương trình mặt phẳng 2D cho quả trứng. Tất nhiên, mình không thể nào tự nghĩ ra được rồi. Search google thì có một trang web “chuyên bán trứng” mathematische-basteleien.de và trong vô vàn phương trình mà họ đưa ra, mình đã tìm chọn quả trứng đơn giản nhất với phương trình như sau:
\[x^2 + y^2 = 2^y\]Vậy đã, xong có được phương trình mặt cắt của quả trứng rồi, bây giờ ta bắt đầu xoay nó thôi!!!
Đại số tuyến tính
Ta có thể vẽ mặt cắt này trên mặt phẳng 2D với các điểm $(x, y)$
\[(x, y, z) = (\sqrt{2^y - y ^ 2}, y, 0)\]Như đã nói ở trên, ta sẽ cho mặt cắt này quay quanh một trục nào đó. Giả sử ta muốn cho mặt cắt này quay quanh trục $y$ với một góc là $\theta$ độ. Ta sẽ có được các điểm $(x, y, z)$ mới như sau: Sử dụng ma trận quay trong không gian 3 chiều:
\[(\sqrt{2^y - y^2}, y, 0) \cdot \begin{pmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{pmatrix} = ((\sqrt{2^y - y ^ 2}) \cdot \cos(\theta), y, (\sqrt{2^y - y ^ 2}) \cdot \sin(\theta))\]Tương tự như vậy, ta sẽ muốn xoay quanh 2 trục còn lại lần lượt một góc là $A$ và $B$ để quả trứng chuyển động một cách “3D” nhất có thể.
\[(\sqrt{2^y - y ^ 2}, y, 0) \cdot \begin{pmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos(A) & \sin(A) \\ 0 & -\sin(A) & \cos(A) \end{pmatrix} \cdot \begin{pmatrix} \cos(B) & \sin(B) & 0 \\ -\sin(B) & \cos(B) & 0 \\ 0 & 0 & 1 \end{pmatrix}\]Và cuối cùng, ta sẽ có được các điểm $(x, y, z)$ mới như sau:
\[x = (\sqrt{2^y - y ^ 2}) \cdot \cos(\theta) \cdot \cos(B) + (\sqrt{2^y - y ^ 2}) \cdot \sin(\theta) \cdot (\sin(B)) - y \cdot \cos(A) \cdot \sin(B)\] \[y = (\sqrt{2^y - y ^ 2}) \cdot \cos(\theta) \cdot \sin(B) - (\sqrt{2^y - y ^ 2}) \cdot \sin(\theta) \cdot (\cos(B)) + y \cdot \cos(A) \cdot \cos(B)\] \[z = (\sqrt{2^y - y ^ 2}) \cdot \sin(\theta) \cdot \cos(A) + y \cdot \sin(A)\]Wait … Cơ mà ta đang biểu diễn trên mặt phẳng 2D mà z lại không bằng 0 thế kia thì làm kiểu gì ???. Lúc này, ta phải dùng tới một kỹ thuật gọi là Z-buffering.
Z-buffering
Về cơ bản, Z-buffering là một kỹ thuật dùng để xác định pixel nào sẽ được hiển thị trên cùng khi nhiều bề mặt 3D chồng lên nhau tại cùng một vị trí (tọa độ x, y) trên màn hình.
Mỗi pixel trong framebuffer (bộ đệm hình ảnh) sẽ có một giá trị độ sâu tương ứng trong Z-buffer (bộ đệm độ sâu). Khi chương trình vẽ một điểm mới, nó sẽ:
Tính khoảng cách từ điểm đó đến người quan sát (thường gọi là giá trị z, hoặc z-depth).
So sánh giá trị z này với giá trị đã lưu trong Z-buffer tại vị trí đó.
Nếu điểm mới gần hơn (z nhỏ hơn), nó sẽ:
- Cập nhật ký tự hiển thị trong framebuffer.
- Ghi lại giá trị z mới vào Z-buffer.
- Nếu điểm mới xa hơn, nó sẽ bị bỏ qua vì đã bị điểm phía trước che khuất.
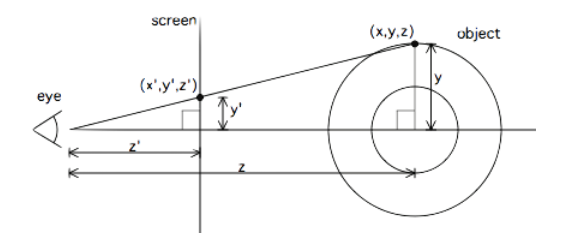
Hãy cùng quan sát hình sau:
Khi chúng ta muốn chiếu một vật thể 3D lên mặt phẳng 2D, bạn cần chiếu (project) các điểm (x, y, z) trong không gian 3 chiều lên thành tọa độ (x', y') trong không gian 2 chiều.
Giả sử có một mặt phẳng z' đơn vị trước mắt người quan sát. Khi nhìn từ trên xuống, ta sẽ chỉ thấy được trục y và z. Ta dễ dàng có được tỉ lệ như sau từ cặp tam giác đồng dạng:
Rút ra được
\[y' = \frac{yz'}{z}\]Tuong tự như vậy với trục x ta cũng có được
Do z' là hằng số, ta sẽ chọn hằng số K1 để tiện tính toán, ta có:
Tuy nhiên, có các điểm chung tọa độ (x, y) nhưng có các giá trị z khác nhau (độ sâu khác nhau). Khi đó ta dùng Z-buffer để xử lý. Cụ thể ta ghi lại giá trị z của điểm gần nhất vào Z-buffer. Nếu có một điểm khác có cùng tọa độ (x, y) nhưng có giá trị z lớn hơn thì ta sẽ không vẽ nó nữa. Ngược lại, nếu giá trị z nhỏ hơn thì ta sẽ vẽ nó và cập nhật lại giá trị z trong Z-buffer.
Ta sẽ có một biến ooz = 1/z để quản lý độ sâu. Tức là z càng lớn thì càng gần camera hơn và ngược lại.
Độ sáng (Illumination)
Có một thứ ta cần quan tâm là độ sáng giữa các điểm. Ta tính độ sáng L bằng công thức:
Ta sẽ chuẩn hóa độ sáng này về khoảng [0, 11] bằng cách nhân với 8. Sau đó ta dùng bảng mã ASCII để ánh xạ độ sáng này thành các ký tự tương ứng. Ta có bảng mã như sau theo thứ tự từ tối nhất đến sáng nhất:
.,-~:;=!*#$@
Hoàn thành
Vậy là xong, ta giờ việc của ta chỉ là cho nó quay liên tục bằng cách thay đổi các góc $A$, $B$, $\theta$ theo thời gian. Và ta đã có được một quả trứng biết quay.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <unistd.h>
#define screen_width 120
#define screen_height 100
#define pi 3.141592653589793
const float phi_spacing = 0.02;
const float y_spacing = 0.03;
const float K2 = 5;
const float ymin = -2.0;
const float ymax = 2.0;
const float K1 = screen_width * K2 * 1.5 / (8 * 2.5);
void render_frame(float A, float B) {
float cosA = cos(A), sinA = sin(A);
float cosB = cos(B), sinB = sin(B);
char output[screen_height][screen_width];
float zbuffer[screen_height][screen_width];
memset(output, ' ', sizeof(output));
memset(zbuffer, 0, sizeof(zbuffer));
for (float y = ymin; y <= ymax; y += y_spacing) {
float x_squared = pow(2, y) - y * y;
if (x_squared <= 0) continue;
float x = sqrt(x_squared);
for (int sign = -1; sign <= 1; sign += 2) {
float x_signed = sign * x;
for (float phi = 0; phi < 2 * pi; phi += phi_spacing) {
float cosphi = cos(phi), sinphi = sin(phi);
float xp = x_signed * cosphi;
float yp = y;
float zp = x_signed * sinphi;
float x_rot = xp * cosB + zp * sinA * sinB - yp * cosA * sinB;
float y_rot = xp * sinB - zp * sinA * cosB + yp * cosA * cosB;
float z_rot = K2 + zp * cosA + yp * sinA;
float ooz = 1 / z_rot;
int proj_x = (int)(screen_width / 2 + K1 * ooz * x_rot);
int proj_y = (int)(screen_height / 2 - K1 * ooz * y_rot) + 25;
float L = cosphi * sinB - cosA * sinphi;
if (L > 0 && proj_x >= 0 && proj_x < screen_width && proj_y >= 0 && proj_y < screen_height) {
if (ooz > zbuffer[proj_y][proj_x]) {
zbuffer[proj_y][proj_x] = ooz;
int luminance_index = (int)(L * 8);
const char *lum_chars = ".,-~:;=!*#$@";
if (luminance_index >= 0 && luminance_index < 12)
output[proj_y][proj_x] = lum_chars[luminance_index];
}
}
}
}
}
printf("\x1b[H");
for (int j = 0; j < screen_height; j++) {
for (int i = 0; i < screen_width; i++) {
putchar(output[j][i]);
}
putchar('\n');
}
}
int main() {
float A = 0, B = 0;
while (1) {
render_frame(A, B);
A += 0.05;
B += 0.1;
usleep(30000);
}
return 0;
}
Conclusion
Tóm lại, nếu có trứng hãy ăn nó chứ đừng tìm cách xoay nó. Cảm ơn và chúc ngày mới vui vẻ :D